UIUCTF | Crack the Safe - Discrete logarithm adventures
A few days ago UIUCTF was held, which I played solo to try out the crypto challenges. While most of the crypto was simple with no deep explanations being necessary, I felt the last challenge was deserving of a dedicated write-up - to document my descent into madness if nothing else.
If interested in just my solve script, click here. Or click here for the intended solve.
crypto/crack_the_safe
Author: Anakin
62 solves / 69 points
“I found this safe, but something about it seems a bit off - can you crack it?”
Opening up our challenge, we find a single file: chal.py. Let’s see what we’ve got waiting for us:
from Crypto.Cipher import AES
from secret import key, FLAG
p = 4170887899225220949299992515778389605737976266979828742347
ct = bytes.fromhex("ae7d2e82a804a5a2dcbc5d5622c94b3e14f8c5a752a51326e42cda6d8efa4696")
def crack_safe(key):
return pow(7, int.from_bytes(key, 'big'), p) == 0x49545b7d5204bd639e299bc265ca987fb4b949c461b33759
assert crack_safe(key) and AES.new(key,AES.MODE_ECB).decrypt(ct) == FLAG
Seems short and simple at first glance. To recover the flag i.e. find the key we need to first solve a discrete logarithm, somehow. As our p is 192-bits large, we suspect that there’s a better way than spending money on renting a VPS to crack it. And so we turn to our good friends Pohlig and Hellman, and their nice algorithm.
Pohlig-Hellman algorithm
I won’t go too far in-depth regarding this (Wikipedia gives a nice explanation already) so I’ll focus on the core idea instead: if the (multiplicative) order of our generator is a smooth integer (i.e. many ‘small’ factors) then it suffices to solve the DLP under each subgroup generated by each of the factors. Doing so massively speeds up our solving of the DLP in comparison to a more generic approach.
We know that for the numbers modulo a prime \(p\) that \(\varphi{(p)} = p-1\) is usually the multiplicative order. So we check if, for our p, this results in a lot of factors:
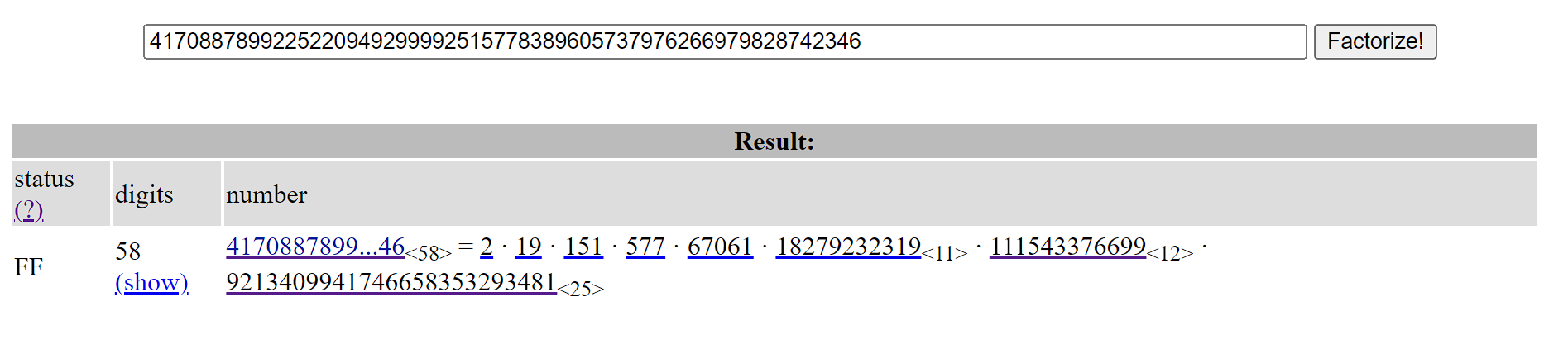
Most seem small, and truly if we just throw them into SageMath, we solve the DLPs in a matter of seconds! Wait, why is the last one taking a while?
What do you mean it’s “too big”?
Yes, our largest factor is, in fact, a bit large. So large that SageMath’s discrete_log couldn’t solve it using its Baby-Step-Giant-Step algorithm for the time it took me to make lunch.
So what now? Do we give up? Fold, and embrace bitter defeat? Give up on CTFs altogether? Well, considering this was the one crypto keeping me from full-solving the category, let’s take a look at the alternatives.
Usually, when faced with something that doesn’t seem to be doable via brute force, you need to consider a smarter approach. Maybe the key is small (i.e. we can get it without solving the last DLP) and we don’t need/care about it? Well…
# g^x = h (mod p)
p = 4170887899225220949299992515778389605737976266979828742347
h = 0x49545b7d5204bd639e299bc265ca987fb4b949c461b33759
g = 7
FF = GF(p)
g = FF(g)
h = FF(h)
n = euler_phi(p) # really just p-1 (alternatively, the multiplicative order of g)
mods = list(factor(n))
mods = mods[:-1] # let's ignore the last one :)
# Pohlig-Hellman implementation (except we skip the largest factor)
xs = []
for (pi, ei) in mods:
gi = g^(n//(pi^ei))
hi = h^(n//(pi^ei))
x = discrete_log(hi, gi)
print(f"x == {x} mod {pi^ei}")
xs.append(x)
key = crt(xs, [a^b for a,b in mods])
assert g^key == h # This fails :(
Right. So we’ll need to solve that last discrete log somehow, and without using SageMath? Sometimes, when faced with something that doesn’t seem to be doable via brute force, you need to consider more brute force.
Now we’re just left to figure out what it is that people usually use for setting all those DLP records… Oh, something called ‘cado-nfs’? - I’ve heard of that before, yeah!
Well, this should be easy. I just go to their website and press the downlo-
…Wait, what do you mean Inria’s GitLab is down?
Beginning of the end
Yeah. During (most?) of the CTF, Inria (the folks behind cado-nfs) had issues with their GitLab resulting in it being offline…

This was an interesting development, but surely - I thought to myself - it didn’t exist just on GitLab, right? And expectedly, someone’s copy was found on GitHub! With their last commit being 4 years ago. And it was impossible to compile on an OS that’s of this decade…
But we’re CTFers! Crypto mains at that! The impossible is just another word for fun, right? And so I went through the painstaking process of building, patching, changing the Makefile - all on the oldest VM instance I had so that it may have a better chance at working (the observant reader might say this part has nothing to do with crypto and it’s just rev, but I disagree: all crypto is rev if you don’t know crypto).
After barely reaching 20% progress during my constant (re-)Make-ing, I begun losing my sanity and - noticing it already having a few dozen solves - I grew certain this wasn’t the way you solve this.
So either you don’t need cado-nfs, or people found a version of it that actually worked and/or patched this monstrosity of a fork. I chose to believe the former, because I really couldn’t find anything to hint at the latter.
Optimizing brute-force
Some months back, during a CTF whose name I cannot recall, my team faced a similar challenge to this one, complete with a large factor for which the DLP wasn’t really solvable. The only addition back then was that our exponent was within a set of given bounds, so there was a trick you could do:
- Use Pohlig-Hellman for the doable factors, leaving you with the knowledge of \(x\) and the modulus in the congruence \(key \equiv x\ \text{mod}\ p_1*p_2*...*p_{i-1}\).
- Keep adding multiples of the modulus to the remainder of the target
- Pray as hard as you can that you hopefully/eventually get a value of \(key\) such that the DLP is ‘solved’
The solution makes sense when you consider that any congruence \(a \equiv b\ \text{mod}\ p\) really just means that there exists an integer \(k\) such that \(a = b + k*p\).
But the real question is: does this work for our situation?
x = 444780066250058017668829040430952
large_factor = 9213409941746658353293481
p = 4170887899225220949299992515778389605737976266979828742347
FF = GF(p)
h = FF(1798034623618994974454756356126246972179657041628028417881)
g = FF(7)
found = False
i = 0
# Our modulus:
delta = p // large_factor
# Then we just let this run for a bit
while not found:
i += 1
x += delta
found = g^x == h
if i % 10000 == 0:
print(i)
print(x)
As it turns out, yes! The while-loop terminates in just a few seconds, and it turns out our \(k\) was around 400,000, which was quite small (and kinda lucky).
Side-note: When solving a DLP with known (or small) bounds then one can employ something like the kangaroo algorithm.
…And this was how I solved it initially. But then an emptiness filled me. Was this it? All that research into suspicious Russian and Korean forks of cado-nfs for nothing?
Let’s explore the intended way of solving the problem, without relying on an odd assumption.
How-to: cado-nfs
First, a short Q&A with myself:
Q: Where do I acquire a functional copy of cado-nfs?
A: Cross the seven seas of Version Control Systems, and at the gates inscribed in poorly-translatable Mandarin, defeat the ogre standing in your way using all of your Google-fu prowess.
Q: I’m serious.
A: There’s actually a GitHub with cado but up-to-date. I did not find it and instead used the arch linux package of cado + patching it slightly so it actually compiles.
Q: Is there a tutorial on how to use cado?
A: Probably.
Q: …Can I have a link to it?
A: It’s supposedly on the GitLab (that is/was unavailable). Make do with the ReadMe’s and pray you don’t need to debug anything.
…With that out of the way, let’s look at cado-nfs properly. After running make & make install and getting something we can actually use, we run ./cado-nfs.py.
Usually, cado-nfs is used for factoring composite integers. But factoring and solving the DLP are two very interlinked problems, and as it turns out cado has a DLP mode enabled with the -dlp flag. It asks us of three things: a target, an ell parameter, and our modulus.
The target was the hex from the crack_safe function, and our modulus was given to us as well. So we’re left to wonder wtf is ell? After a few minutes of reading cado’s (kinda confusing?) ReadMe for the DLP mode, it turns out it corresponds to the order of a subgroup. In other words, we just plug in our largest factor of \(p-1\) in there and that’s it!
> ./cado-nfs.py -dlp -ell 9213409941746658353293481 target=1798034623618994974454756356126246972179657041628028417881 4170887899225220949299992515778389605737976266979828742347
And… wait, where exactly do we supply our generator? How does cado know what to use?
Fun with logarithms
So cado actually uses a ‘random generator’ (base), presumably one that works ‘best’ for solving the DLP. In the output, it tells you what base it used. But that’s a bit problematic for us because we kinda want it to be ours. So what are we supposed to do?
After running cado, it gives us the option to rerun the ‘snapshot’ but with a different target (or multiple targets) - this is because the pre-descent stuff is the hardest part of solving a DLP with a NFS, and that’s independent of the target. I mention this because it allows us to recompute another target with the same base very quickly.
And this is important why? Recall the logarithm identities, notably the following:
\[\log_b c = \frac{\log_a c}{\log_a b}\]What this means is that if we compute the (discrete) logarithm for our desired target, and then for our desired base (in our case: 7), then simply by dividing the two (modulo our subgroup) we get our desired logarithm!
Let us call the logarithm for our desired target logtarget and for our generator logg. Then, in Sage, it’d look something like this:
E = GF(ell)
logtarget = E(logtarget)
logg = E(logg)
secret = logtarget * logg^-1 # 741784031885807265615861
And secret is our remainder! All that’s left now is to combine this with our initial Pohlig-Hellman code from above, getting us the following solve script:
p = 4170887899225220949299992515778389605737976266979828742347
h = 0x49545b7d5204bd639e299bc265ca987fb4b949c461b33759
g = 7
FF = GF(p)
g = FF(g)
h = FF(h)
n = euler_phi(p)
mods = list(factor(n))
# Pohlig-Hellman
xs = []
for (pi, ei) in mods[:-1]: # We now know our x for the last factor!
gi = g^(n//(pi^ei))
hi = h^(n//(pi^ei))
x = discrete_log(hi, gi)
print(f"x == {x} mod {pi^ei}")
xs.append(x)
xs.append(741784031885807265615861) # From cado-nfs / the previous snippet
key = crt(xs, [a^b for a,b in mods])
assert g^key == h
print(key)
And using the key to decrypt the AES ciphertext, we really do get our flag: uiuctf{Dl0g_w/__UnS4F3__pR1Me5_}. Solved, now with cado-nfs!